How to Measure the Height of A Building/Tower or Skyscraper | How to Find the Height of Object/Building by using Theodolite

In this Article today we will talk about the how to measure the height of a building | how to measure elevation of Building | angle of depression calculator | how to measure a building | height of a house | building height measurement | height of building | How is Building Height measured | Broomstick Method

How to Calculate Height of a Building or Tower:

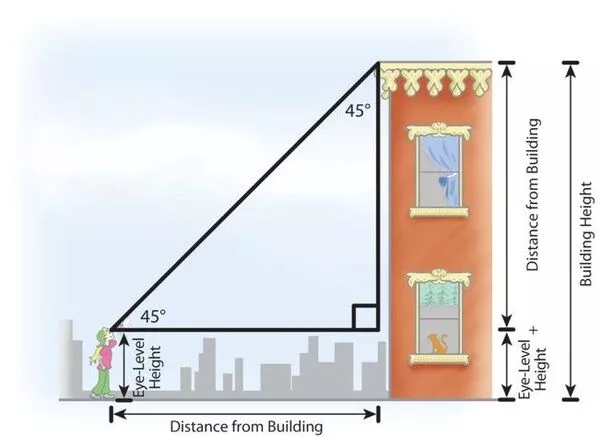
Sometimes we may need to find the height of a building before or after construction. There are several ways to calculate building height. In this article, I will use two methods: how to measure elevation of Building

Trignometry Method for Calculating the Height of Building/Tower (Method 1):

This is the simplest method. you can use this method to find out the height of any object such as building or tower, water tank, tree, lighthouse etc. angle of depression calculator

Required Data:

Distance and Angle (As shown in fig)

Given:

Angle = Ɵ = 30^o Distance – d – 5000 feet

Procedure:

We Know, height of a house

Tangent = The Ratio of the opposite side to the adjacent side.

which means tanƟ = Opposite side / Adjacent Side

here Ɵ = 30^o

So, Tan = 30^o = Opposite side / Adjacent Side = x/d = x/5000

x = tan 30^o x 5000 = 0.577 x 5000 = 2885 feet

Hence the Height of the Building/Tower is 2885 feet. height of a house

---

Broomstick Method (Method 2):

It is not always possible to use the above method due to the availability of space or time. This measurement method also uses shadows but you do not have to wait until the length of the broom shadow is equal to its height. Place the broomstick on the floor facing upwards. Now measure the height of the broom and the length of the drop shadow. Quickly measure the length of the shadow created by the structure. With the same triangles, we can reach the height of the building. building height measurement

To understand the properties of similar triangles, see the image below. The structure and its shape form a right-angled triangle. And the broomstick and its shadow form the same triangle of right angles. Since both triangles have the right angles, they are the same.

The height of the structure can therefore be calculated from the ratios stated below.

(Broomstick’s shadow length/ Broomstick’s height) = (Building’s shadow length/ Building’s height)

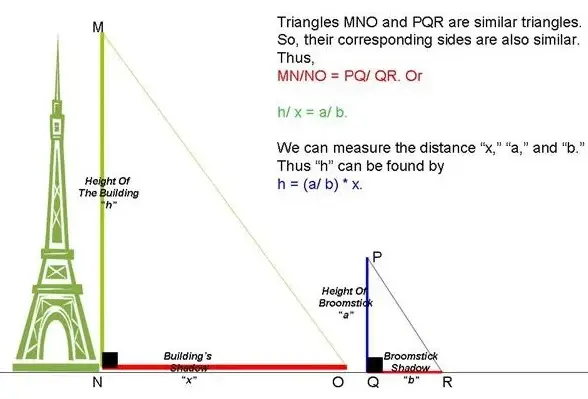
As per the above formula; h/x = a/b

Required Data:

Suppose, x = 600 ft and a = 100 ft, b = 60 ft then, find x = ?

Procedure:

As we know that,

h/x = a/b

so, h = (a/b) * x = 100/60 x 600 = 1000 ft

Hence the Height of the Building/Tower is 1000 feet.

---

How to Measure the Height of Object/Building by using Theodolite (Method 3):

Now let’s calculate the height of a building using theodolite as shown below.

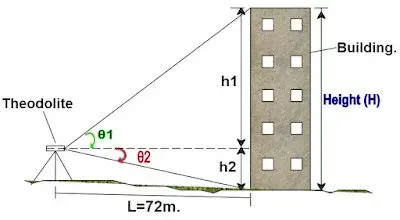
First, you should measure the theodolite on a straight axis and set the angle to 0 ° on the horizontal axis e.g shown as a dotted line. You must measure the distance (L) of the building from the location of the theodolite channel as shown in the diagram.

Place the balance in the upper corner of the building using theodolite and write down the value of the angle θ1. Similarly, bisect the bottom edge corner of the building and write down the value of angle θ2.

Let’s draw the triangles above for the purpose of calculating the values ​​of the measured angle. Broomstick Method

Let’s say triangle 1 is like ABC, where A is the point of the theodolite channel.

Triangle ABC :

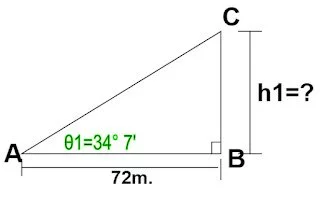
Angle θ1 = 34° 7′

Length AB = L = 72m.

From trigonometry,

Tan θ1

= opposite side ÷ adjacent side.

= side BC ÷ side AB

Tan 34° 7′

= h1 ÷ 72m.

h1 =  tan 34° 7′ × 72m.

= 0.67747 × 72m

= 48.778m.

Let us name triangle 2 as ABD, where A is the theodolite station point.

Triangle ABD.

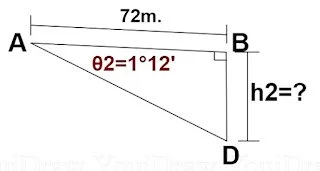
Given data:

Angle θ2 = 1° 12′

Length AB = L = 72m.

From trigonometry,

Tan θ2 =

opposite side ÷ adjacent side.

= side BD ÷ side AB

Tan 1° 12′

= h2 ÷ 72m.

h2 =  tan 1° 12′ × 72m.

= 0.02094 × 72m

= 1.508m.

Now, the height of building

H = h1 + h2

= 48.778m. + 1.508m.

 = 50.286m.

---

OTHER POSTS:

1. Load Calculation on Column, Beam, Wall & Slab

2. Basic Rules for Design of Column | Thumb Rules for Column Design

3. Basic Components of Road Structure and Method of Construction

4. How to Create Road Alignment Coordinates Report XML XLS in AutoCAD Civil 3D

5. Difference Between Flexible and Rigid Pavement | Types of Pavement

---

Conclusion:

Full article on how to measure the height of a building | how to measure elevation of Building | angle of depression calculator | how to measure a building | height of a house | building height measurement | height of building | how is building height measured | How is Building Height measured | Broomstick Method. Thank you for the full reading of this article in “The Civil Engineering” platform in English. If you find this post helpful, then help others by sharing it on social media. If any formula of BBS is missing from this article please tell me in comments.