Bar Bending Schedule Calculation Basic Formulas:
The Bar Bending Schedule Formulas are mathematical calculations used to determine the proper dimensions and quantities of steel bars, or rebars, needed for a construction project. These basic bbs formula are an integral part of the bar bending schedule. With the help of these formula we can do the cutting length or reinforcement calculation in Excel. Also discuss about how to make bar bending schedule reinforcement calculation.
What is Bar Bending Schedule (BBS) ?
A Bar Bending Schedule is the process of bending and cutting of the reinforcement bar into the required shape (according to the drawing requirement) and making It includes information about the:
- Location & Marking of Bar
- Type of Bar
- Size of Bar
- Cutting Length of Bar
- Number of Bar
- Bending Detail of Bar
- Total Quantity
of each bar in a reinforcement drawing of a building structure. This process of listing is called Scheduling.
Steps in preparing a bar bending schedule (BBS) using formulas:
We should follow the following steps during the preparation of bar bending schedule:
- Inspect each face’s concrete cover.
- Inspect each structural element’s tension and compression bars’ lapping lengths.
- Verify each bar’s bent direction.
- Arrange the structural components by floor. For instance, before moving on to the next floor, all ground floor components must be planned, and all footing must be completed before moving on to the starter columns.
- The bar mark must climb steadily starting at 01 points.
- Solid understanding of the details and factors influencing the actual construction.
- Double-check the bar bending schedule calculation to ensure accuracy and minimize errors.
- Review the bar bending schedule to ensure that it is complete and accurate.
- Use the bar bending schedule as a reference during the construction process to guide the workers in cutting, bending, and placing the rebars.
Basics of Bar Bending Schedule Formulas | BBS Calculation Formulas:
Diameter of Reinforcement Bars in MM:

Standard Length of Bar in Meter:

Diameter of Reinforcement Bars in Inches/No’s:

Standard Length of Bar in Feet:

Weight of Steel Bar Formula Per Meter (Kg/m):

| Diameter of Bar (mm) | Unit weight in kg/m |
| 8 | 0.395 |
| 10 | 0.617 |
| 12 | 0.889 |
| 16 | 1.580 |
| 20 | 2.469 |
| 25 | 3.858 |
| 32 | 6.321 |
| 40 | 9.877 |
Weight of One Steel Bar in Kg/Bar Formula:

Weight of Steel Bar Formula Per Feet (Kg/ft):

Weight of One Steel Bar in Kg/Bar Formula:

Cutting Length of Main Bar with Hook Formula:

Where, L = Span – (Conc. Cover x 2), Note: Hook Length in Stirrups should be 10d or 75mm, where d is dia of bar.
Cutting Length of Main Bar with Bend Formula:

Where, L = Span – (Conc. Cover x 2), if you need bend deduction then you should deduct 4d (2d + 2d) for two 90 Deg bends from main bar cutting length.
Overlapping Formula :

Concrete Cover or Clear Cover in Reinforcement:

Clear Cover for:
- Footing: 50mm
- Column: 40mm
- Beam: 25mm
- Slab: 20mm
- Staircase: 15mm
- Chajja: 15mm
- Pile: 60mm
- Pile Cap: 60mm
Spacing in Reinforcement:

Number of Bars Formula:

Number of Stirrups Formula:

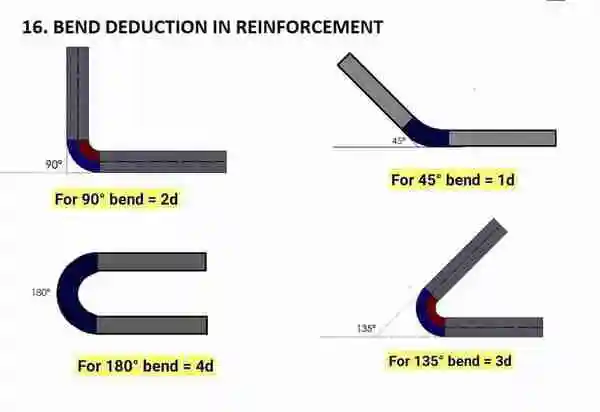
Bend Deduction Formula in Bar Bending:
Bend increases the length of bar. So we need lesser length than we see in the drawing. So cutting length is taken less then the required length:
Cutting Length of Crank or Bent Up Bar Formula:
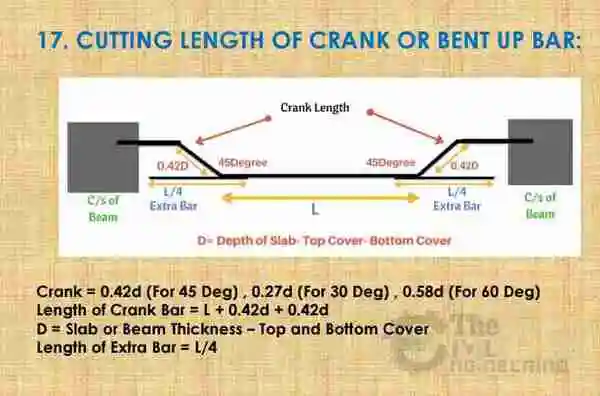
Bend Deduction: If you need bend deduction then you should deduct 4d (1d + 1d + 1d + 1d) for four 45 Deg bends from crank or bent up bar cutting length.
Cutting Length of Rectangular Stirrups Formula:
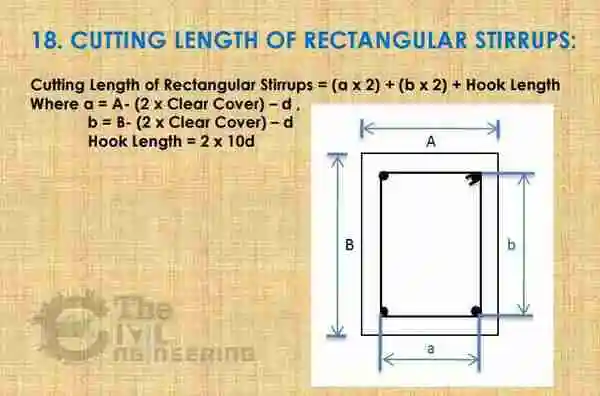
Bend Deduction: If you need bend deduction then you should deduct 6d (2d + 2d + 2d) for three 90 Deg bends & 6d (3d + 3d) for two 135 Deg hook bends from rectangular stirrup cutting length.
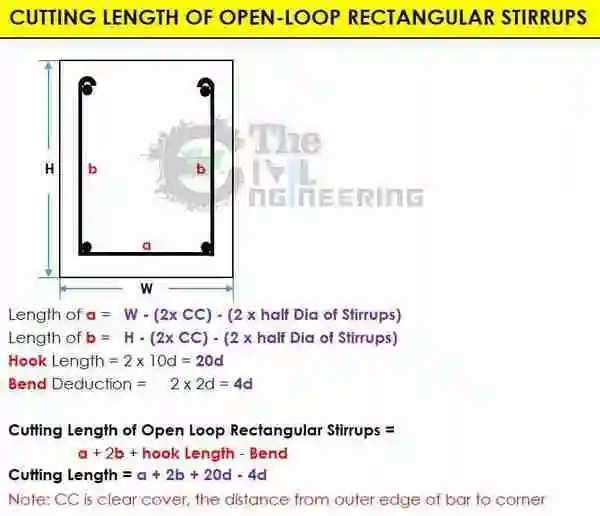
Cutting Length of Open-Loop Rectangular Stirrups Formula:
Cutting Length of Triangular Stirrups Formula:
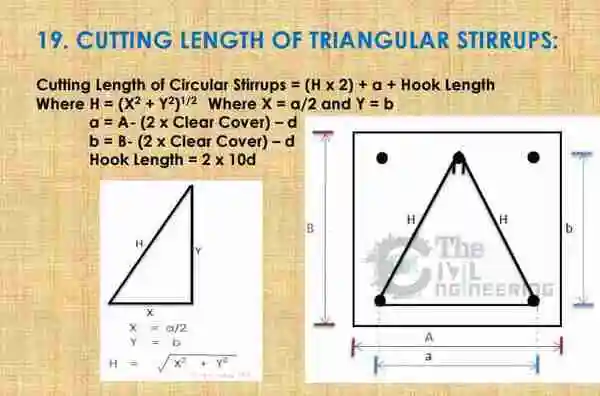
Bend Deduction: If you need bend deduction then you should deduct 12d (3d + 3d + 3d + 3d) for four 135 Deg bends from triangular stirrup cutting length.
Cutting Length of Circular Stirrups Formula:
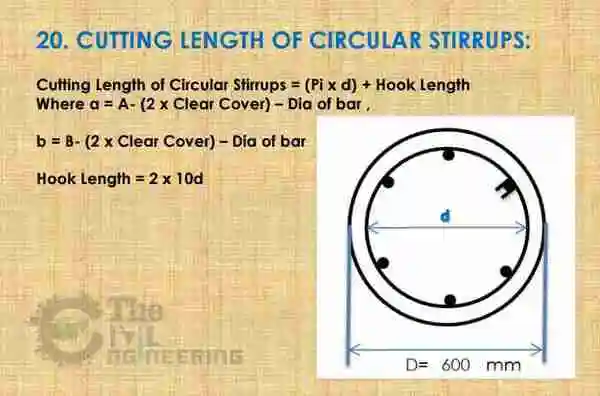
Bend Deduction: If you need bend deduction then you should deduct 6d (3d + 3d) for two 135 Deg hook bends from circular stirrup cutting length.
Cutting Length of Diamond Stirrups Formula:
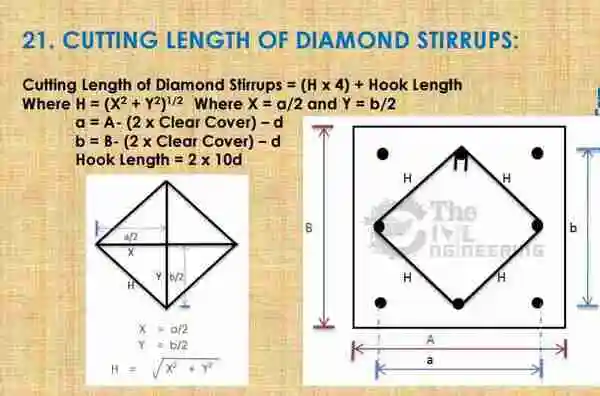
Bend Deduction: If you need bend deduction then you should deduct 6d (2d + 2d + 2d) for three 90 Deg bends & 6d (3d + 3d) for two 135 Deg hook bends from diamond stirrup cutting length.
Cutting Length of Spiral or Helix Stirrups Formula:
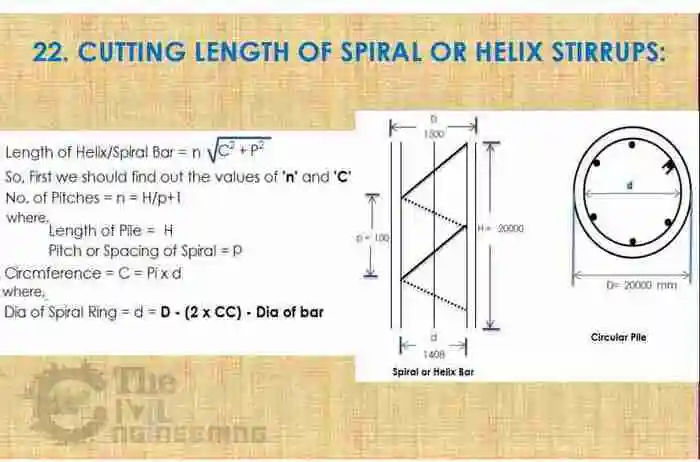
Bend Deduction: If you need bend deduction then you should deduct 6d (3d + 3d) for two 135 Deg hook bends from spiral ring cutting length.
Cutting Length of Chair Bar Formula:
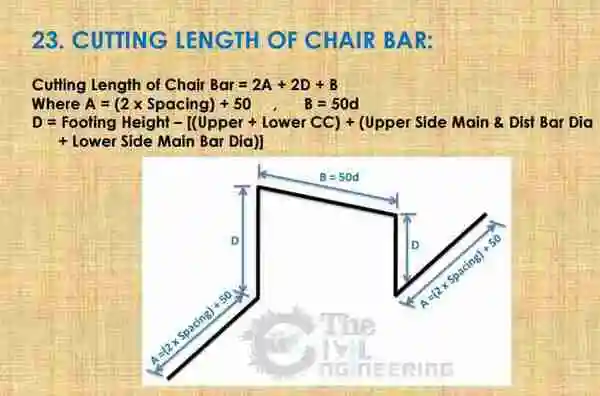
Bend Deduction: If you need bend deduction then you should deduct 8d (2d + 2d + 2d) for four 90 Deg bends from chair bar cutting length.
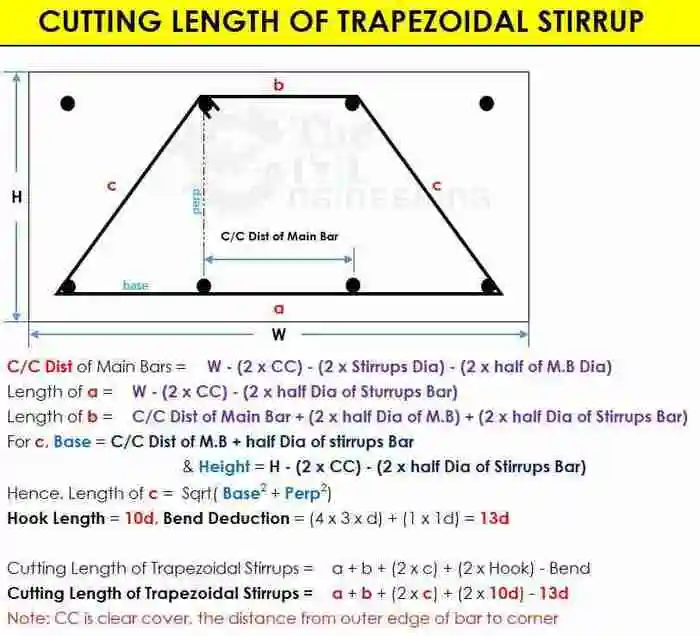
Cutting Length of Trapezoidal Stirrup Formula:
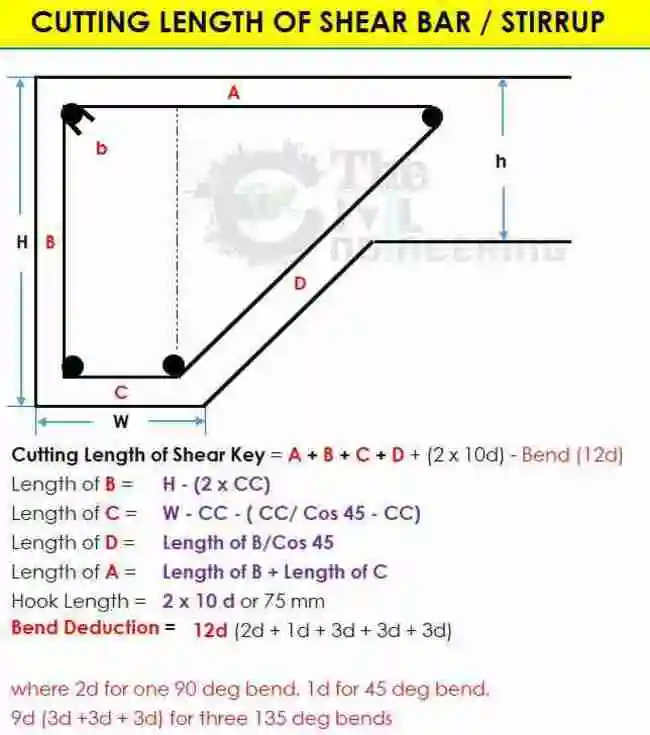
Cutting Length of Shear Key Bar or Stirrup Formula:
Cut Length of Haunch Bar Formula:
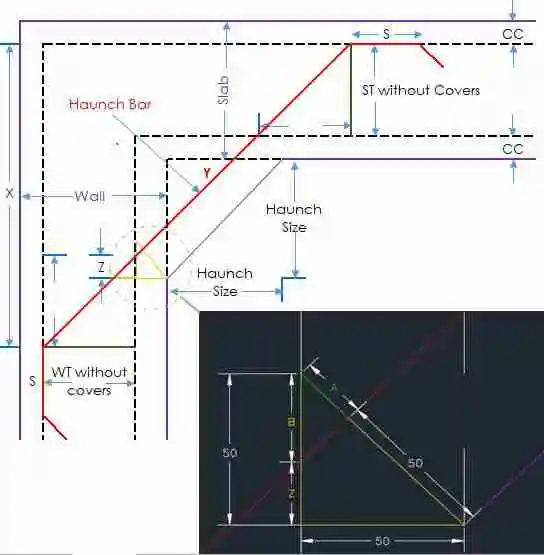
Cutting Length of Haunch Bar = S + Y + S (Where S is given as lap)
As we Know that
Y = X / Cos 45
X = (Thickness of wall – Slab Cover) + (Haunch Size) + (Wall Thickness without covers – Z)
Where, Z = Cover – B
B = A / Cos 45 A
we can find the A by using Pythagoras theorem Hyp2 = Base2 + Perp2
For More detail please see the Mathematical Example
Bend Deduction: If you need bend deduction then you should deduct 2d (1d + 1d) for two 45 Deg bends from haunch bar cutting length.
Cut Length of Bracket Bar Formula – Case 1:
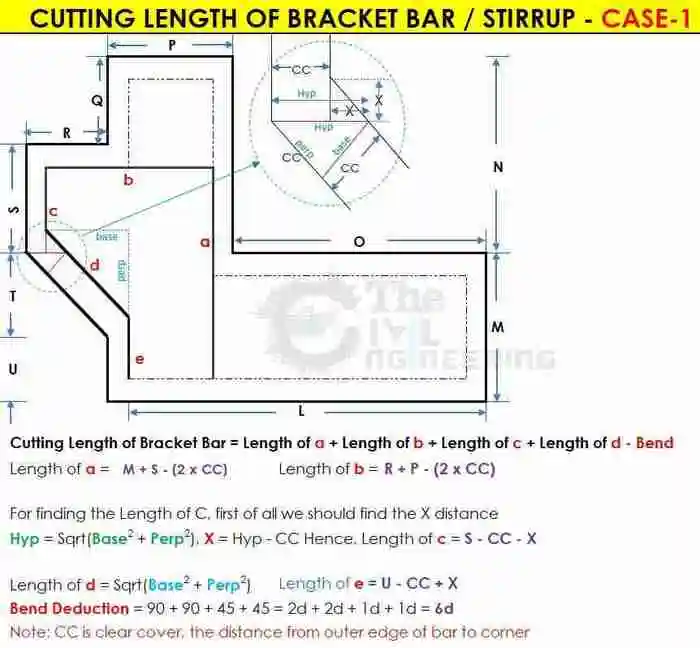
Cut Length of Bracket Bar Formula – Case 2:

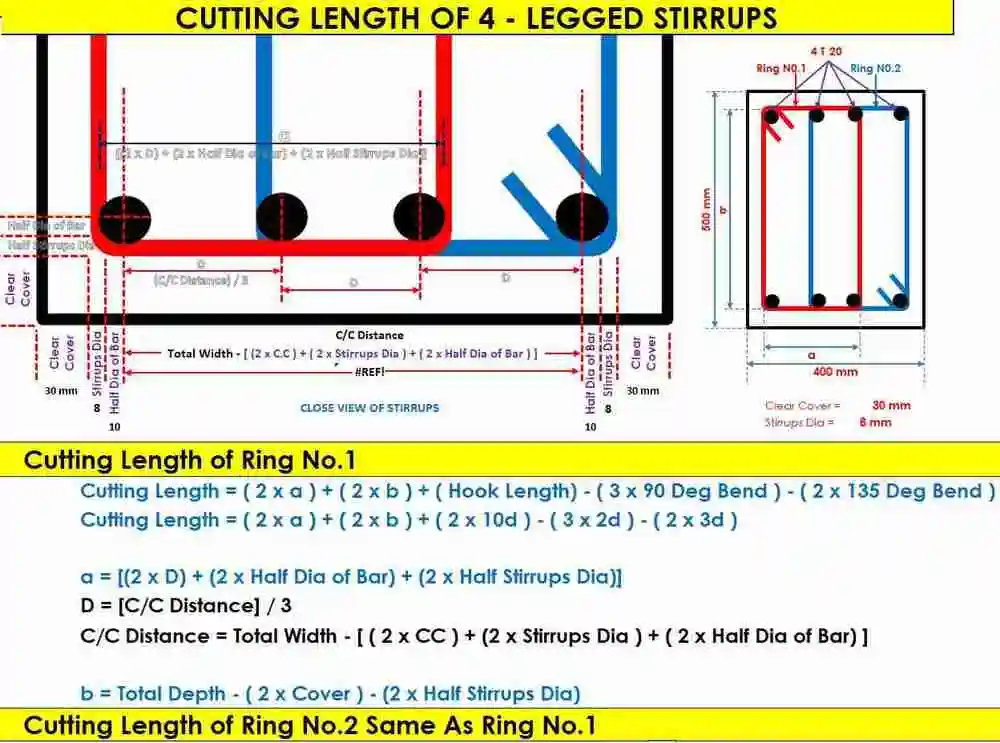
Cut Length of Four Legged Stirrups Formula:
Cut Length of Six Legged Stirrups Formula:
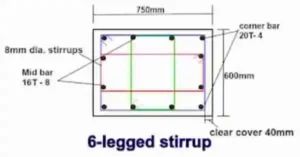
For Calculating the Cutting Length of Stirrups, First of all we convert the stirrups in three parts (Stirrups 1, Stirrups 2, Stirrups 3)
Cutting Length of 6-Leggeed Stirrups = Length of Stirrups 1 + Length of Stirrups 2 + Length of Stirrups 3
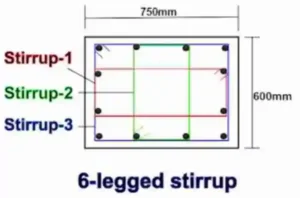
Cut Length of Stirrups 1:
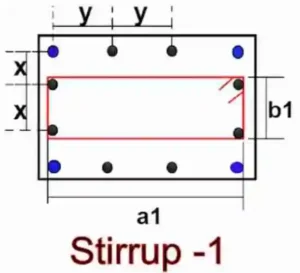
Cut Length Formula for Stirrup-1:
= [(2nos × a1) + (2nos. × b1) + (2nos. × hook length) – {(3nos. × 90° bend )+ (2nos. × 135° bend)}]
First, we will calculate the value of a1 & b1 a1 = [(column width ) – {(2nos. × clear cover) + (2nos.× 1/2 dia. of stirrup-1 bar)}]
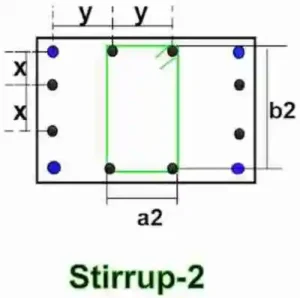
Cut Length Formula for Stirrup-2:
Cutting Length Formula for Stirrup-3:
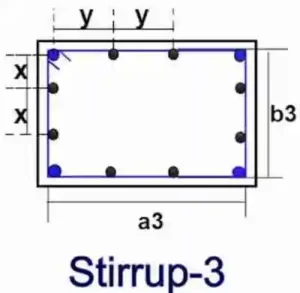
= [(2nos.× a3) + (2nos. × b3) + (2nos. × hook length) – {(3nos. × 90° bend )+ (2nos. × 135° bend)}]
First, we will calculate the value of a3 & b3
a3 = [(column width ) – {(2nos. × clear cover) + (2nos.× 1/2 dia. of stirrup-3)}]
b3 = [(column depth ) – {(2nos. × clear cover) + (2nos.× 1/2 dia. of stirrup-3)}]
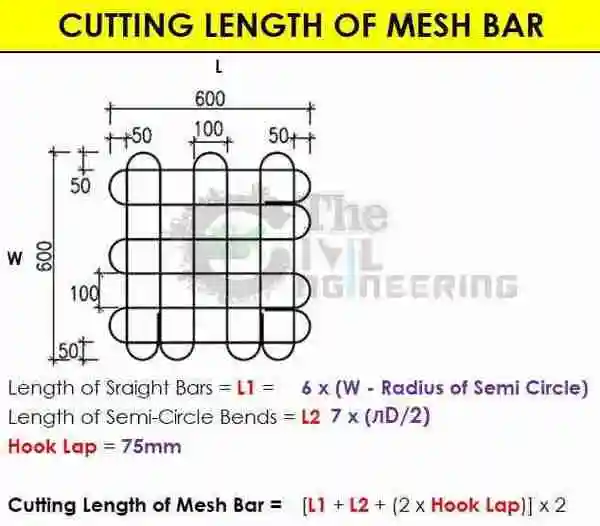
Cut Length of Mesh Bar Formula:
Volume of Steel Reinforcement for Different RCC member:
| RCC Member | Volume of Steel by volume of Concrete |
| Slab | 1.5% – 2% |
| Column | 2.5% – 3% |
| Beam | 2.5% – 3% |
For Example,
for 10 M3 concrete in Column, considering 2.5% of steel Volume, the column has a 0.25 M3 of steel. Calculate the total weight of steel and steel weight per M3.
Volume of Steel for 10m3 Concrete = 0.25 m3
Wight of Steel Per M3
Concrete = total Volume of steel X Density of Steel (i.e. 7850 Kg/M3)
Weight of steel for 10 M3 concrete = 0.25 X 7850 = 1962.5 Kg.
For 10 m3 Concrete,
the total steel required is 1962.5 Kg. For 1 m3 Concrete, the total Steel required is 196.25 Kg.
Rolling Margin of Reinforcement Steel Bar Formula:
Cut reinforcement bar into 3 pieces, each length 1 meter Weight Each piece differently i.e. 10 mm Día Bar,
1st one weight 0.617,
2nd one weight 0.62,
3rd one weight 0.625
Now Calculate the rolling margin of Reinforcement bar

Standard Hook and Bend Length Formula as per ACI 318:
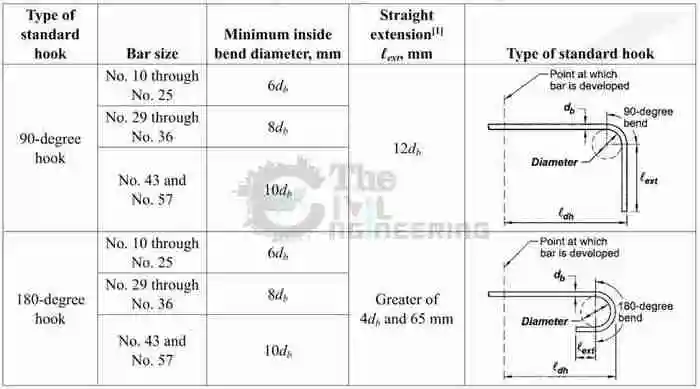
Development Length for Reinforcement Bars:
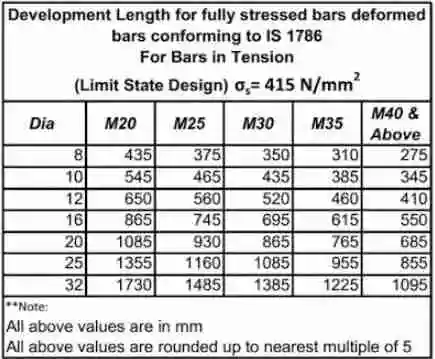
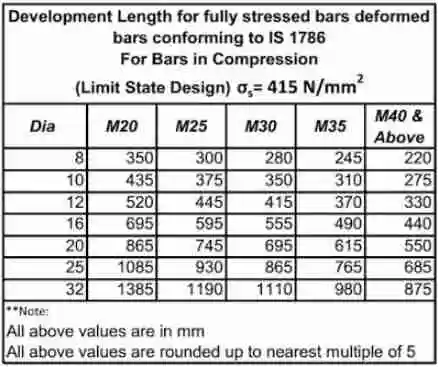
Advantages of Bar Bending Schedule:
- Cutting Length and Bending of Reinforcement can be done.
- BBS helps to avoid wastage of steel reinforcement and reduces project costs.
- It helps to accurately estimate the steel reinforcement requirements for each structural member.
- BBS is useful for auditing the reinforcement and checking for theft or pilferage.
- It makes it easy and quick to prepare construction work bills for clients and contractors.
Why Steel is Used as Reinforcement:
- Strong enough for cost-effective design of reinforced concrete structures.
-
Concrete is a weak material in tension, but steel has very good tensile strength. Therefore, steel is used in the tension zone.
-
The temperature coefficients of steel and concrete are nearly equal;.
-
when concrete shrinks in setting time, it provides proper bonding between steel and concrete.
-
Modulus of Elasticity of Steel is very high; this means that it can withstand great deformation without any permanent damage to itself.
Types of Reinforcement Bars:
- Fe-250
- Fe-415
- Fe-500
Conclusion:
In conclusion, bar bending schedule formulas are essential for construction projects. They help in determining the correct quantity and size of steel bars, as well as calculating the cutting lengths and weight of each bar. Overall, bar bending schedules are a crucial aspect of any structure and should not be overlooked.
OTHER POSTS:
-
How to Calculate the Cutting Length of Spiral Bar or Helix Bar | BBS
-
How to Calculate Cutting Length of Stirrups
-
Difference between Plinth Level, Ground Level, Sill level and Lintel Level
-
How to Calculate Unit Weight of Steel Bars | Steel Weight Formula
-
How To Find Out The Cutting Length Of Main Bars & Circular Rings
-
Bar Bending Schedule (BBS) | BBS Step by Step Preparation | Excel Sheet
-
Bar Bending Schedule Basic Formulas | BBS Formula | What is BBS


10 Comments
Hi
Hii
Thanks for the comments please visit more articles by clicking on “All Posts” tab of the Menu Bar
Hello Sir, There is no Excel sheet attached to any BBS video Sir, Please upload all Excel sheets with their particular video, Sir
Sir plz share Whatsapp group
Thanks for the comments please visit more articles by clicking on “All Posts” tab of the Menu Bar
Hi Waseem Raja,
I really appreciate your educational post on civil perspectives. I am an Electrical Engineer and do learn alot of all you are posting.
Thanks for the comments please visit more articles by clicking on “All Posts” tab of the Menu Bar
Thank sir for your knowledge sharing.
Thanks for the comments please visit more articles by clicking on “All Posts” tab of the Menu Bar